Chapitre 9 Probabilité, première
Les probabilités se font avant une expérience, elles prévoient les Statistiques

Les probabilités: notions à connaître
Univers: Ensemble de tout les résultat de l'expérience
Éventualité/issue: Un résultat d'expérience aléatoire
Évènement: Ensemble d'éventualité (= subdivision d'un univers
Évènement impossible: Univers exclus de toutes les éventualités
Ensemble A et B incompatible : A∩B = Ø
Ensemble A complémentaire de B: A∩B = U (univers)
➥AUB = Ø et A se note $B↖ {-} $(B barre ou /B en informatique)
I Variable aléatoire
1) Définition
-Une variable aléatoire discrète est une fonction qui associe à chaque issue un réel
➥Notée X, elle englobe toute l'expérience
-xi est le réel associé à l'issue i
2) Loi d'une variable aléatoire
On associe à une valeur xi une probabilité d'apparition notée p(X=xi) ou pi
➥Se lit: probabilité que le résultat de X soit xi
Exemple: on tire un dés à 6 faces, on choisis xi=6
-p(X=6): $1/6$ (ou p(xi = $1/6$)
3) Espérance de X
C'est le nombre vers lequel tend la moyenne X quand le nombre de répétition d'expérience est très élevé
E[X] = $∑↙{i=1}↖n$ (xi ✕ p(xi))
➥C'est la somme des éventualités (résultats) marqués de leur probabilité
➨On obtientune sorte de moyenne des résultat d'une expérience aléatoire
4) Variance V
Comme pour les statistiques, la variance sert à calculer l'écart type
V(X) = $ ∑↙{i=1}↖n$ (p(xi) ✕ (xi-E[X])²)
➥Somme d'une issue moins l'espérance au carré, multiplié par la probabilité d'apparition de xi
Écart type
σ = √V(X)
➥C'est la moyenne des écarts entre le résultat xi et l'espérance E[X]
Propriétés:
-On peut transformer une variable X en fonction affine, avec a et b des réels
Y: une autre variable aléatoire
Y = aX+b
➥b symbolise la valeur de départ
➥a symbolise un coefficient
➨Cela permet de mettre en relation 2 expérience aléatoire
-On dit qu'une expérience aléatoire est égale à une autre coefficientée
➥On peut donc les comparer, cela évite aussi de refaire des expériences car il suffit de mettre un coefficient
On a aussi:
E(Y) = a ✕ E[X]+b
V(Y) = a² ✕ V(X)
➥Les coefficients s'appliquent aussi aux calculs de variance, d'espérance
➨On peut donc aussi comparer des écarts type et espérance de deux expériences différentes
II Loi binomiale
1) Épreuve de Bernoulli
-On appel "épreuve de Bernoulli", une expérience aléatoire qui:
-N'as que 2 issues et qui sont contraire
➥S (Succès) l'issue favorable
➥E (Échecs) l'issue défavorable (= non S ou $S↖{→}$)
-On note la probabilité de succès "p"
➥La probabilité d'échecs est donc: 1-p
Schéma de Bernoulli
-On appel schéma de Bernoulli une répétition de n épreuves de Bernoulli
➥Ces épreuves doivent être identiques et indépendante
2) Définition de la loi binomiale
X: variable aléatoire égal au nombre de succès obtenus dans un schéma de Bernoulli de "n" épreuves où la probabilité est de "p"
-La loi binomiale de X est notée: B(n;p)
-On déduit la probabilité de X à l'aide l'arbre (cf plus pas)
➥ On compte le nombre de chemins menant à X succès
➥On applique le principe multiplicatif aux probabilités de chaque branche du chemin
3) Représentation du schéma de Bernoulli par un arbre pondéré
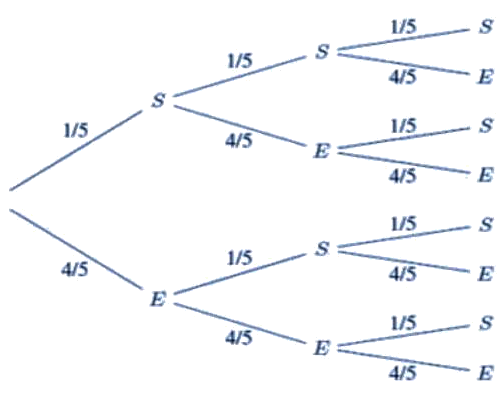
-On multiplie les probabilités quand on avance sur une branche
4) Coefficient binominaux
Soit k un nombre entier inférieur ou égale à n
-On appel coefficient binomiale le réel noté $(\table n;k)$
➥Se lit de "k" parmi "n"
-C'est le nombre de chemin qui réalisent k succès parmi n épreuves de Bernoulli
Propriétés: $(\table n;1) = n$
$(\table n;n) = 1$
$(\table 0;0)$ = 1
(\table n; k ) = (\table n;n-k)$
➥Il y a autant de chemin conduisant à k succès qu'à k échecs
Pour calculer ce nombre, on utilise la calculette, cela s'appelle "combinaison" (math,probabilité,combinaison)
Exemple: 5 combinaison 2 = (52) = 10
5) Théorème de la loi binomiale
Pour tout entier k: nombre de succès, inférieur ou égale à n
Calcule de probabilité de la loi B(n;p)
p(X=k) = $(\table n;k)$ ✕ pk ✕ (1-p)n-k
6) Triangle de Pascal
Propriété: $(\table n+1;k+1) = (\table n;k)+ (\table n;k+1)$
On a donc un tableau de type: pour k allant de 0 à 5 et n allant de 0 à 5
| n\k | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 1 | - | - | - | - | - |
| 1 | 1 | 1 | - | - | - | - |
| 2 | 1 | 2 | 1 | - | - | - |
| 3 | 1 | 3 | 3 | 1 | - | - |
| 4 | 1 | 4 | 6 | 4 | 1 | - |
| 5 | 1 | 5 | 10 | 10 | 5 | 1 |
III Echantillonage
-Intervalle de fluctuation de p de 95% d'une variable aléatoire X:
B(n;p): [$a/n ; b/n$]
Avec a: plus petit entier qui vérifie p(X≤k)>0,025
Avec b: plus grand entier qui vérifie p(X≤k)≥0,975
La suite du cours: les Statistiques
-
Partagez ce cours !
Suivez Nicolas KRITTER sur google + ( cours inspiré de celui fait par le professeur de la classe)
