Opération sur les matrices |cours de spé maths terminale

Cours et code réalisé par Vincent Maffet

I Opération sur les matrices

1) Addition et multiplication par un réel

Additionde matrices: Définition:

Si A = (a_ij) et B = (b_ij) deux matrice de même taille (m*n) alors leur somme A+B ets définie par:

A+B = (c_ij) où c_ij = a_ij + b_ij

➥ On additionne les termes des matrices ayant la même position i,j pour former la matrice du résultat

➥ On peut donc additionner les matrices que si elles sont de même taille

Mulitplication par un réel, définition:

Soit une matrice A= (a_ij) de taille m*n et λ un réel

la matrice λA est la matrice (b_ij) tels que b_ij = λa_ij

➥Quand on multiplie une matrice par un réel, On multiplie tous les termes de cette matrice par ce nomre réel

REMARQUE:

Les règles de priorités des additions et mulitplications sont les même qu'avec des réels

2) Multiplication d'une matrice ligne par une matrice colonne

n un entier naturel non nul

A = (a_1,j une matrice ligne avec n colonnes (1 ✕ n)

B = (b_i,1 une matrice colonne avec n lignes (n ✕ 1)

On a donc: A ✕ B = [a_1,1 ,a_1,2 , ... a_1,n] = $(\table b_{1,1} ; b_{2,1} ; ⋮ ; b_{n,1})$ = a_1,1 ✕ b_1,1 + a_1,2 ✕ b_2,1 + a_1,n ✕ b_n,1

Ce qui donne: A ✕ B = $∑↙{k=1}↖n$ (a_1,k ✕ b_k,1)

Exemple:

(1 4) ✕ $(\table -5 ; 3)$ = 1 ✕ (-5) + 4 ✕ 3 = 7

(2 -3 1) ✕ $(\table 4 ; 2 ; 0)$ = 2 ✕ 4 + (-3) ✕ 2 +1 ✕ 0 = 2

3) Multiplication de deux matrices

Définition

Soit n un entier naturel non nul.

Soit A = (a_1,j) une matrice ligne de n termes et B = (b_i,1) une matrice colonne de n termes

Alors A ✕ B est un nombre et A ✕ B = _{i = 1}Σⁿ(a_1,i*b_i,1)

➥ On ne peut multiplier des matrices colonnes que par des matrices lignes (ou des réels, cf plus haut)

➥ les 2 matrices doivent avoir le même nombre de terme

4) Puissances d'une matrice

a) Matrice diagonale

Définition :

- Une matrice diagonale est une matrice carrée dont tous les coefficients qui ne sont pas situés sur sa diagonale principale sont nuls.

- Une matrice diagonale d'ordre n dont tous les coefficients diagonaux sont égaux à 1 est appelée matrice unité. Elle est notée I_n.

b) Puissances d'une matrice

Définition :

A désignant une matrice carrée, on définit A² par A² = A ✕ A et tout entier naturel p, A^p = A*A*...*A } p fois

Propriété :

Soit D une matrice diagonale, pour tout n ∈ N, Dⁿ est une matrice diagonale obtenue en élevant à la puissance n les coefficients de D

5) Matrice inversibles et application aux systèmes linéaires

a) Matrice inversible

Propriété-définition :

Soit A une matrice carrée d'ordre n, n ∈ N*, on dit que A est inversible lorsqu'il existe une matrice carrée d'ordre n : B telle que AB=BA=I_n

La matrice B est alors unique et appelée matrice inverse de A. On note A^-1.

Propriété admise :

Pour montrer que la matrice A carrée d'ordre n est inversible, de matrice inverse B, il suffit de montrer que AB=I_n ou BA=I_n

Propriété-définition :

Soit A une matrice carrée d'ordre 2,

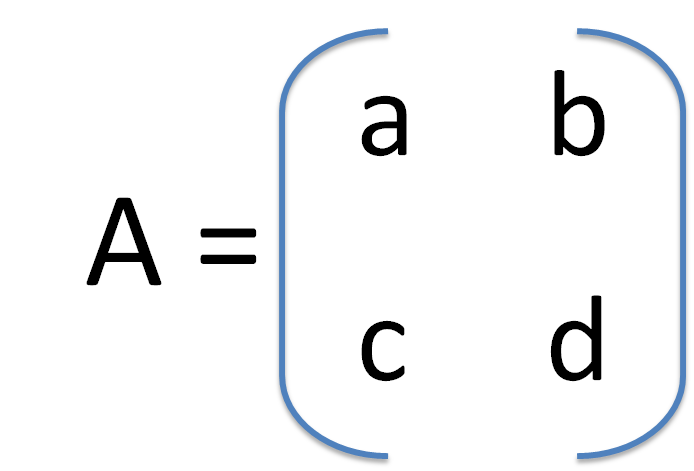
La matrice A est inversible si et seulement si ad-bc≠0

Le réel ad-bc est appelé déterminant de la matrice A

Si ad-bc≠0 alors :

Démonstration :

Soit

A = $(\table a , b ; c , d )$

B = $(\table d , -b ; -c , a )$

A ✕ B = $(\table a , b ; c , d ) ✕ (\table d , -b ; -c , a )$

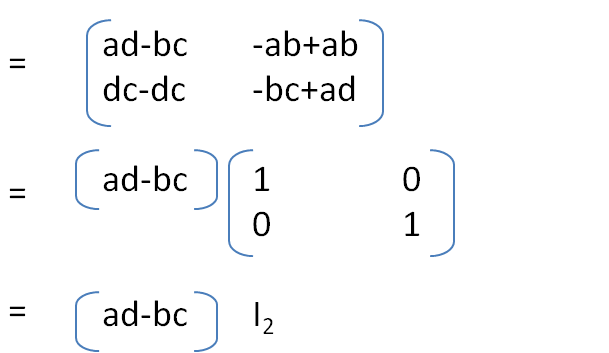
Si ad-bc≠0 alors A ✕ $1/{ad-bc}$ ✕ B=I₂ donc A est inversible

et

Si ad-bc=0 alors A ✕ B =O₂ et A n'est pas inversible

En effet si A était inversible, d'inverse C, on aurait CAB=CO₂=0 et CAB=(CA)B=B=0 car CA=I₂ ce qui n'est pas le cas.

b) Application aux systèmes linéaires

Propriété :

Un système linéaire à n équations et n inconnues x₁, x₂ ... x_n

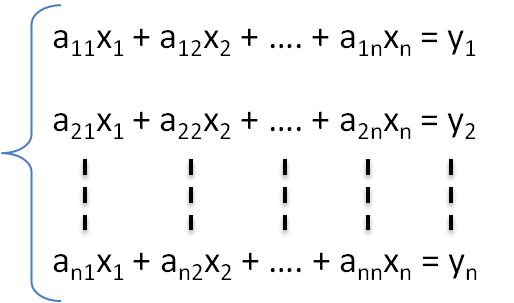
peut s'écrire sous la forme matricielle AX=Y où A=(a_ij) est une matrice carré d'ordre n, X=(x_i) et Y=(y_i) sont des matrices colonnes de taille n*1

Si A est inversible, le système admet une solution unique donnée par X=A^-1Y

Démonstration :

Si A est inversible,

Si AX=Y alors (A^-1A)X=A^-1Y et X=A^-1Y

A^-1Y est l'unique solution du système qui s'écrit sous forme matricielle AX=Y

-

Partagez ce cours !

Suivez Vincent Maffet sur google + ( cours inspiré de celui fait par le professeur de la classe)