Satellites et planètes

Les lois d Kepler

1ère loi de Kepler: loi des ellipses

O: le centre de l'ellipse

F: un foyer de l'ellipse

a: Moitié grand axe

b: Moitié petit axe

b = a ✕ √ (1-e²)

OF': OF = e ✕ a

e: l'excentricité de l'ellipse, 0<e<1

REMARQUE: pour un cercle, e = 0

Loi de Kepler:

La trajectoire d'une planète autour d'un soleil est une ellipse, la planète est l'un des foyers de cette ellipse

➥Il en est de même pour les satellites autour de la terre

REMARQUE: On considère que certaine planète ont un mouvement circulaire par rapport au soleil (comme la terre) car l'excentricité de l'ellipse est très faible

➥ Pour la terre: e =0,02

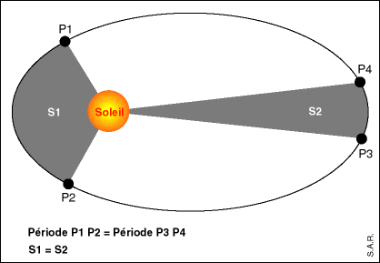
2ème Loi de Kepler: Loi des aires

Les aires balayée par le rayon Soleil-Planète pendant une durée identique sont égales

Le point le plus proche est appelé le périgée

Le point le plus loin est appelé l'apogée

➨La vitesse la plus élevée est atteinte au périgée

➨La vitesse la plus faible est atteinte à l'apogée

REMARQUE: si la trajectoire est quasi-circulaire, alors la vitesse est quasi-constante

3ème Loi de Kepler: loi des périodes

Relation entre T et a

$ {T²}/{a^3}$ = constante

T: Période révolution

a: Moitié grand axe de l'ellipse

REMARQUE: Si le mouvement est quasi circulaire alors on considère que a = R (rayon)

Rappel: loi de gravitation universelle

Rappel: F_A/B = -F_B/A

La loi de gravitation universelle:

F_A/B = ${(G \; ✕ \; M_A \; ✕ \; M_B )}/{r^2}$

r: la distance de A à B en m

Ma: masse de a en kg

G = 6.67 ✕ 10^-11 U.S.I

➥Remarque G est différent de g

Exemple: au voisinage de la terre:

$ {(G \; ✕ \; M_{terre}) }/{r^2} = 9.81 m.s^{-2}$ (environ)

➥M_Terre masse de la terre et r: le rayon de la terre

Pour que la force soit non négligeable, il faut que les masses soient considérables (ex celle des astres)

Approximation du mouvement circulaire

On considère pour la suite que le mouvement est circulaire donc: a = R

Repère de Freinet

Base (u_t;u_n) orthonormé, placé sur l'objet en mouvement

u_n: Vecteur unitaire perpendiculaire à la trajectoire, dirigé vers le centre de rotation

u_t: Vecteur unitaire tangent à la trajectoire

->On place le repère sur le centre de l'astre en rotation

R: le rayon (distance astre-centre de rotation)

Équation de l'accélération:

$ a = v'.u_t \; + \; ({v'}/{R}).{u_n}↖ {→}$

Composante du vecteur a:

a_t = v'

➥Dérivée de la vitesse

a_n = ${v²}/R$

Application de la troisième loi de Newton

Référentiel: héliocentrique

On place le référentiel sur la terre

S: soleil, T: terre

On a donc:

F_S/T = $ m \; ✕ \; a = ({G \; ✕ \; M_t \; ✕ \; M_s}/{r^2})\; ✕ \; {u_n}↖ {→} $

➥ a = $(G ✕ Ms)/{r²} ✕ {u_n}↖ {→}$

Composante du vecteur a:

a_t = 0

a_n = $G ✕ {M_S}/{r²}$

Comme v' = 0 (a_t = 0) alors le mouvement est circulaire uniforme

➥L'accélération est nul

➥ v est constante

Donc $G ✕ {M_S/r} = {v²}/r$

La vitesse v est donc: v = $√({G ✕ M_S}/r)$

La vitesse v de la terre est appelé vitesse de satellisation circulaire

Retour sur la 3ème loi de Kepler

Rappel: vitesse = distance/temps

Donc ici: $ v = {2π R}/{T}$

➥T: la période révolution, 2πR: distance parcourue (rotation autour du soleil)

Comme le mouvement est quasi-circulaire:

${T²}/{a^3} = {T²}/{E^3}$

➥E: le rayon

Comme T = ${2ΠR}/v$ alors: $T² = {4Π^2 R^2}/{v^2} = {4Π^2R^3}/{G ✕ M_S}$

Donc T²/R³ = 4Π²/(G ✕ M_s) = constante

Donc la relation ${T²}/{a^3}$ donne bien une constante

➥La 3ème Loi de Kepler est vérifiée

Cas des satellites terrestres

Lancement d'un satellite autour de la terre

V₀: vitesse de lancement du satellite

V_satcir: vitesse de satellisation circulaire

V_libération = vitesse de libération

V₀< V_satcir: retour sur terre

V₀ = V_satcir: Mouvement circulaire

V_satcir < V₀ < V_libération: Mouvement elliptique

V₀ > V_lib: Le satellite échappe à l'attraction terrestre

Remarque: V_libération = √(2) ✕ V_sat

➥La marge pour envoyer un satellite autour de la terre est faible

satellite géostationnaire

Période du satellite: environ 24H

➥ T_sat = 24H

M_t: Masse de la terre

Donc ${T²}/{R^3} = {4Π²}/{G ✕ M-t}$

Remarque: T est en secondes

➨ r³ = ${G ✕ {M_t}²}/(4Π²) $= 4,2 ✕ 10⁴Km

Il faut ensuite enlever le rayon de la terre

➥ R correspond à la distance de centre à centre

Donc l'altitude du satellite est de: 42 000-6400 = 35 600km

-

Partagez ce cours !

Suivez Nicolas KRITTER sur google + ( cours inspiré de celui fait par le professeur de la classe)