Phénomènes ondulatoire

Diffraction
Mise en évidence expérimentale
Expérience avec une cuve à onde
Quand la fente est plus large que la longueur d'onde, l'onde est diaphragmée

Quand la fente est moins large que la longueur d'onde, l'onde est diffractée

Diffraction avec un laser, étude la figure de diffraction
On fait passer un laser à travers une fente et on observe la tâche lumineuse sur l'écran
On observe une tâche central et des tâches secondaires, qui sont de plus en plus petites
Plus l'ouverture de la fente est petite, plus les phénomènes sont importants

a: épaisseur de la fente
D: distance entre la fente et l'écran
L: largeur de la tâche centrale
θ: angle de diffraction
λ: longueur d'onde du laser
REMARQUE: la distance laser-fente ne change rien
On arrive à la relation: $ θ = λ/a $
Avec θ en radian et λ et a qui doivent avoir la même unité
Relation entre l'angle θ la distance D et la longueur de la tâche centrale L:
$ tan(θ) = L/{2 \; ✕ \; D}$
REMARQUE: quand θ est beaucoup plus petit que 1, on a tan (θ) ≈ θ
On a donc la relation:
$L = {(2 \; ✕ \; λ\; ✕ \; D)}/a$
Interférences lumineuse
Expérience des fentes de Young
On fait passer un laser à travers 2 petites fentes très proches et on regarde le résultat sur un écran
On voit des interférences: les tâches centrales et secondaires sont subdivisées entre frange lumineuse et frange sombre

a: largeur des fentes
D: distance entre les fentes et l'écran
i: interfrange, c'est la distance qui sépare 2 frange claire (ou sombre) consécutives
REMARQUE: les franges claires et les franges foncées sont de la même taille
Comme i est très faible, on mesure la taille de 10 franges, puis on la divise par 10 pour avoir l'interfrange
Conditions d'interférences
Pour qu'il y ai une interférence, il faut que les deux ondes soient synchrone et aient la même fréquence
➥Les lumières doivent être cohérente (= issue de la même source)
Différence de marche
On projette un laser à travers deux fentes très proches et ont regarde leurs diffraction
➥Ces deux fentes se comportent comme des sources de laser

a: largeur des fentes
P: point sur l'écran, d'ordonnée y
S2P: distance entre la fente S2 et P
S1P: distance entre la fente S1 et P
D: distance entre la fente et l'écran
b: distance qui sépare les deux fentes
Formule de la différence de marche:
Différence de marche delta entre la source S1 et S2 au point P
y: ordonnée du point et D: distance écran-fente
$ δ = S_2P-S_1P = {(b \; ✕ \; y_p)}/{D}$
Si δ = k ✕ λ (on multiplie par un entier la longeur d'onde), on a alors des interférences constructives
➥Les ondes sont en phase
➨On obtient des franges brillantes
Si $δ = (2k\; + \;1)\; ✕ \; λ/2 $
(on multiplie par un nombre non entier la longeur d'onde), on a alors des interférences destructives
➥Les ondes sont en opposition de phase (elles s'annulent)
➨On obtient des franges noir
Démonstration de l'interfrange
Pythagore:
(S2P)² = $D²+(y+(b/2))^2$ et (S1P)² = D²+$(y-(b/2))^2 $
δ = $(S_2 P - S_2 P) \; ✕ \; ((S_2P + S_1 P)/(S_2 P+S_1 P))$
Donc: δ = $((S_2 P)^2 -(S_2 P)^2)/(S_2 P+S_1 P)$
➥ δ ≈ ${(y+b/2)^2-(y-b/2)^2}/{2D} = {2yb}/{2D} = {yb}/D$
On peut donc en déduire:
Ordonnée de la 1ère frange brillante:
y1 = ${δ_1 \; ✕ \; D}/b = {λD}/b$ car on a k = 1
y2 = ${δ_2 \; ✕ \; D}/b = {2λD}/b$ car on a k = 2
Formule d'interfrange:
i = y2-y1 = ${λD}/b$
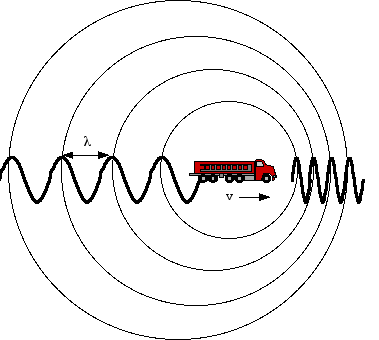
Effet Doppler
Définition
Une onde émise à la fréquence fe est perçue à une fréquence fr différente de fe quand l'émetteur et le récepteur sont en mouvement l'un par rapport à l'autre
Démonstration
v: la vitesse de l'émetteur
D: distance entre l'émetteur et le récepteur
Soit:
fe: fréquence de l'onde émise par l'émetteur
C: vitesse de l'onde
Expérience:
L'émetteur émet le premier maximum à t0 = 0
Le récepteur reçoit le premier maximum à t1 = $D/C$
L'émetteur émet le deuxième maximum à t2 = Te (=période l'onde)
Le récepteur reçoit le deuxième maximum à t3 = Te+ $((D \; ✕ \; v \; ✕ \; Te)/C)$
$(D \; ✕ \; v \; ✕ \; Te)$: distance parcourue par le récepteur durant l'intervalle de temps Te
$(D \; ✕ \; v \; ✕ \; Te)/C$ :temps de parcours de l'onde pour arriver au récepteur
La période perçue par le récepteur est: Tr = t3-t1 = Te+$(D/C)-((v \; ✕ \; Te)/C)-(D/C) = Te - ((v \; ✕ \; Te)/C)$
➥ Donc Tr = Te ✕ ${1-v}/C$
La fréquence perçue en fonction du mouvement de l'émetteur:
Dans le cas où l'émetteur se rapproche du récepteur:
fr = $fe/(1-(v/C))$
➥Le son est plus aigu car la fréquence perçue est plus élevée: fr > fe
Dans le cas où l'émetteur s'éloigne du récepteur:
fr = $fe/(1+(v/C))$
➥Le son est plus grave car la fréquence perçue est plus basse: fe > fr
-
Partagez ce cours !
Suivez Nicolas KRITTER sur google + ( cours inspiré de celui fait par le professeur de la classe)