Physique terminale: Mouvement dans un champ de force uniforme

Mouvement en champs de pesanteur

Rappel sur le champ de gravitation

On se place à une altitude inférieure à 10 km

On considère le champ de pesanteur comme constant, on a:

g = 9.81 m.s^-2

➥g: le vecteur du champ de pesanteur

Le poids (p) est la force que subit toutes masse dans le champ de pesanteur

On a: p = m ✕ g

p en N, m en Kg et g en m.s^-2

Chute libre sans frottement

Exemple avec la chute d'une bille:

Système: bille, Référentiel: terrestre

Au temps t=0 on lâche la bille d'une altitude z = 0

➨La vitesse est donc égale à 0

Bilan des actions mécaniques:

Comme un néglige les frottements, on a qu'une seule force qui s'applique sur la bille: sont poids (p)

Bilan des forces:

Comme on néglige les frottements, on a:

$∑{F_{ext}}↖ {→}$ = p

On utilise la 2ème loi de Newton (voir le cours précédent), on trouve donc:

$∑{F_{ext}}↖ {→}$ = m ✕ a = p

➥Donc p = m ✕ a

Or, comme p = m ✕ g, on a donc: a = g

➨L'accélération est égal au vecteur champ de pesanteur

➨La masse n'as aucune influence

Composante du vecteur a:

/x: a_x = 0

/y: a_y = 0

/z: a_z = g

➨ La bille n'accélère que sur z

Composante du vecteur v:

/x: v_x = V0x = 0

/y: v_y = V0y = 0

/z: v_z = a ✕ t+V0z = a ✕ t

Composante du vecteur OG:

/x: v_x = X0 = 0

/y: v_y = Y0 = 0

/z: v_z = $(a ✕ t²)/2 $+V0 ✕ t+Z0 = $(g ✕ t²)/2$

On détermine les valeurs des constantes grâce aux conditions initiales

Ici: On part du point (0;0;0) à vitesse nulle donc V0 = 0 et x0=y0=z0=0

Chute avec frottement

On étudie la chute d'une bille dans un fluide

à t0: v0 = 0 et x0=y0=z0=0

n est dans la situation où: $∑{F_{ext}}↖ {→}$ = m ✕ a

Bilan des actions mécaniques:

P: le poids (vers le bas, proportionnelle à la masse): m ✕ g

Pa: la force d'Archimède (vers le haut, proportionnelle à la masse): mf ✕ g

f: les frottements (vers le haut, proportionnelle à la vitesse): k ✕ v

On a donc: m ✕ a = P+Pa+f

➥ m ✕ a = m ✕ g - m_f ✕ g - k ✕ v

Comme on a qu'un seul mouvement et qu'il est sur l'a_x e z on a:

a_z = $g(1-{m_f}/m)-(k/m)$ ✕ k ✕ v_z

Remarque: on note $g(1-{m_f}/m)$: A et ($k/m$): B

On a donc: a_z = A-B ✕ v_z

A: pesanteur dans le liquide, B: force de frottement

On en déduit donc que plus la vitesse augmente, plus l'accélération diminue

➥Quand A = B ✕ v_z , alors la vitesse est constante

➨On atteint la vitesse limite maximum quand a = 0

REMARQUE: la masse a de l'influence sur la vitesse limite

➥Plus la masse est grande, moins elle est sensible aux frottements

Mouvement parabolique

On se place dans un repère orthonormé, y dirigé vers le haut et x dirigé vers la droite

On tire un projectile quelconque

Le vecteur vitesse forme un angle de α

A t=0: x0 = y0 = 0

Bilan des Actions Mécaniques:

Le poids: P=m ✕ g

On projette le vecteur V0 sur l'a_x e des abscisses et sur l'a_x e des ordonnées

Donc: V0x = ‖V0‖ ✕ cos (α)

Donc: V0y = ‖V0‖ ✕ sin (α)

On néglige les frottements donc: $∑{F_{ext}}↖ {→}$ = m ✕ a = m ✕ g

➥ a = g

Composante du vecteur a:

/x: 0

/y: -g

/z: 0

➨Il n'y a aucune force qui s'exerce sur le solide appart le poids

Composante du vecteur vitesse:

/x: V0x = ‖V0‖ ✕ cos (α)

/y: a ✕ t+V0y = - g ✕ t+ ‖V0‖ ✕ sin (α)

/z: 0

Composante du vecteur du déplacement:

/x: $(‖V0‖ ✕ cos (α) ✕ t)/2$ + x0

/y: ${-g ✕ t²}/2$ + ‖V0‖ ✕ sin (α) ✕ t + y0

/z: 0

Équation de la trajectoire

On a $t = x/(‖V0‖ cos(α)$ donc l'équation du mouvement est:

y = $(a ✕ x²)/(‖V0‖ cos(α))/2$ + tan(α)

Mouvement en champs électrique uniforme

Rappel sur les champs électriques uniforme

E: le vecteur du champ électrique

REMARQUE: la direction de E est du + vers le -

On a la relation: F = q ✕ E

➥ q: la charge

On néglige le poids quand on s'intéresse aux forces électriques

➥ 10¹⁰ fois inférieur à la force F

Canon à électron

On fait traverser un électron d'un point A sur une plaque à un point B sur une autre plaque, séparée par une distance D

➥A et B sont sur la même droite, il n'y aura donc qu'un mouvement sur x

Électron: -e

e = 1,6 ✕ 10^-9

m = 9.81 ✕ 10^-31 kg

U = 3000V

D: distance entre les deux plaques

A t =0: x = 0 et v0 = 0

On a: ∑ F_ext = m ✕ a = F

ET F = -e ✕ E

On a un seul mouvement, qui est sur l'a_x e x

Donc: a_x = $(e ✕ E)/m = (e ✕ U)/(m ✕ D)$

➥On remplace E par $U/D$

➨ a est constante et positive car E est une constante négative

On a: v_x = ${(e ✕ U)/(m ✕ d)}$ ✕ t

On a: x = ${e ✕ U ✕ t²}/{2 ✕ m ✕ D}$

Calcul de la vitesse en sortie (point B sur la deuxième plaque)

t1, le temps que x = D (que l'électron aille de l'entrée A à la sortie B)

On a donc: D = $(e ✕ U ✕ t²)/(2 ✕ m ✕ D)$

➥ t1 = $√((2 ✕ d ✕ D²)/e ✕ U))$

Comme Vb = V(t1) on a :

Vb = $(e ✕ U)/(m ✕ D) ✕ √((2 ✕ m ✕ D²)/(e ✕ U))$

Donc Vb = $√((2 ✕ e ✕ V)/m)$ = 3,25 ✕ 10⁷m.s^-1

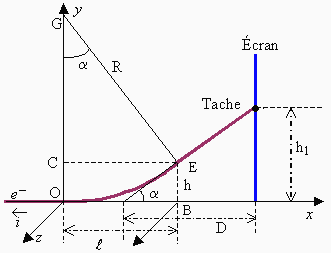
Déviation du faisceau d'e-

On lance un électron sur l'a_x e des x à une vitesse v0 au milieu de 2 plaques (une plaque - en bas et une plaque + en haut)

➥La seul force qui s'exerce sur l'électron est la force électrique qui le dévie

Il y a donc un mouvement sur x ET sur y

Composante du vecteur de l'accélération:

/x = a_x =0

/y = a_y = $(-e ✕ E)/m$

Composante du vecteur vitesse

/x: v_x = v_x 0

/y: v_y = $(-e ✕ E)/m$ ✕ t +v_y 0 = $(-e ✕ E)/m$ ✕ t

➥Au départ, v_y 0 = 0

Composante du vecteur de déplacement:

/x : x = V0x ✕ t

/y : y = $(-e ✕ E ✕ t²)/(2 ✕ m)$

Partagez ce cours !

Suivez Nicolas KRITTER sur google + ( cours inspiré de celui fait par le professeur de la classe)