Les Probabilités

Union et évènements

Univers

L'univers contient tous les résultats d'une expérience

Il est souvent noté Ω

Remarque: on appel parfois les résultats: issues, éventualités,possibles...

Évènements

Un évènement est un sous ensemble d'un univers, il contient certains résultats de l'expérience

Exemple: obtenir un chiffre pair sur un lancé de dé

Évènements élémentaires

Un évènement élémentaire est un évènement qui ne contient qu'un seul résultat

Vocabulaire et opération concernant les évènements

Ω :univers, A ⊂ Ω et B ⊂ Ω

Évènements incompatibles (ou disjoint)

Deux évènements sont incompatibles s'ils ne peuvent pas se réaliser en même temps

Évènements contraire

Deux évènements sont contraires si forcément l'un ou l'autre se produit

On note alors: A = $\ov{B}$ (ou B =$\ov{A}$)

➥L'un se produit si l'autre ne se produit pas

Propriété: Si A et B sont contraire, alors ils sont aussi disjoint (=incompatible)

Intersection de deux évènements

L'évènement A ∩, B est réalisé quand A et B sont réalisé en même temps

Réunion de deux évènements

L'évènement A ∪ B est réalisé quand A OU B se réalise

Remarque: c'est un OU exclusif, ce qui signifie donc que c'est l'un ou l'autre, mais pas les deux en même temps

Contraire des évènements A ∪ B et A∩B

On retrouve le théorème de Morgan:

$\ov{(A ∪ B)} = \ov{B} ∩ \ov{B}$

$\ov{A ∩ B)} = \ov{A} ∪ \ov{B}$

Probabilité sur un ensemble

Définition

Ω: un univers de cardinal fini

Cardinal d'un ensemble: nombre d'éléments de l'ensemble

une probabilité est une fonction mathématique

Une probabilité p d'un évènement A dans l'ensemble fini Ω est une application qui fait correspondre à A un réel p(A)

Application: Fonction où tout élément de l'ensemble de départ a exactement une image

Propriétés de l'application

0≥p(A) ≥ 1

p(A): la somme des probabilités de tous les évènements compris dans A

➥1 ou plusieurs évènements élémentaires

p(Ω) = 1

p(∅) = 0

Propriétés des probabilités d'un ensemble

Si A et B sont disjoint alors:

p(A∪B) = p(A) + p(B)

On a donc:

Pour tout évènement A et B:

p(A∪B) = p(A)+p(B)- p(A∩B)

Autres propriétés:

p($\ov{A}$) = 1-p(A)

∅: évènement impossible, ω : évènement certain

P(A) = 0 ➨ A est un évènement presque impossible

P(A) = 1 ➨ A est un évènement presque certain

Pour A et B, deux évènements quelconques:

p(A∩B)+p($\ov{A}$∩B) = p(B)

Généralisation

A1,A2...An: n évènements disjoint 2 à 2 vérifiant:

A1∪A2∪...∪An = Ω

Donc pour tout évènement B ∈ Ω:

p(B) = p(B∩A1)+p(B∩A2)+...+p(B∩An)

Un cas particulier: l'équiprobabilité

On parle d'équiprobabilité quand tous les évènements élémentairess ont la même probabilité de se réaliser

-L'équiprobabilité est indiquée par des expressions comme:

"au hasard", "de façon aléatoire", "dés non pipés"

Propriété:

Dans une situation d'équiprobabilité, la probabilité d'un évènement 1 d'un univers Ω est:

p(A)= ${card(A)}/{card (Ω)}$

Exemple: pour un dés non pipés à 6 faces: p(1) = p(2) = p(3) = p(4) = p(5)=p(6) = $1/6$

➥1 seul évènement élémentaire pour un univers de 6 possibilités

Rappel: un cardinal d'un ensemble fini c'est le nombre d'éléments de l'ensemble

Probabilité conditionnelles

Définition

A et B: deux éléments d'un même univers

On note la probabilité de l'évènement A sachant que B est réalise: p_B(A) et vaut:

p_B(A) = ${p(A∩B}/{p(B)}$

➥Se lit: "probabilité de B sachant A

Exemple: 1 sac avec 4 boules bleu et 3 vertes

Les boules bleues sont numérotées de 1à4 et les boules vertes de 3 à 5

A: "obtenir une boule portant le numéro 3

B: "obtenir une boule bleu"

p_B(A) = $(1/7)/(4/7) = 1/4$

car il y a 4 boules bleues sur 7 boules et 1 boule bleu portant le numéro 3 sur 7 boules au total

Conséquence

A et B: deux évènements de probabilité non nulle

p(A∩B) = p_B(A) ✕ p(B) = p_A(B) ✕ p(A)

➥ p_A(B) = ${p(A∩B)}/{p(A)}$ et p_B(A) = ${p(A ∩ B)}/{p(B)}$

Arbre de probabilité

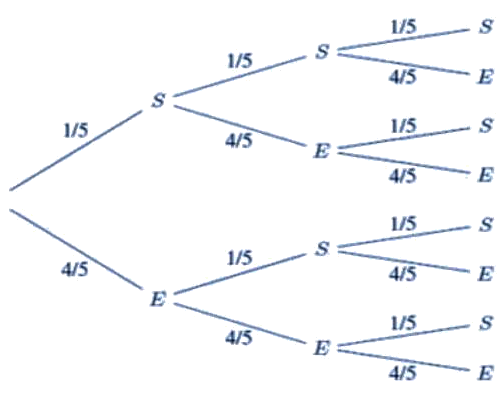
-On multiplie les probabilités quand on avance sur une branche

Propriété

Évènements

A et B sont deux évènements de probabilité non nulle

p($\ov{A}$) = 1-p(A)

➥La somme des 2 branches d'un nœud = 1 (loi des noeuds)

Équiprobabilité

S'il y a équiprobabilité lorsque B est réalisé alors:

p_B(A) = ${card(A ∩B)}/{card (B)}$

Formules des probabilités totales

A₁, A₂...A_n, n évènements disjoints 2 à 2 et de probabilité non nulle

Pour tout évènement B de Ω:

p(B) = p_A1(B) ✕ p(A1)+p_A2(B) ✕ p(A2)+...+p_An(B) ✕ p(An)

$ p(B) = ∑↙{k=1}↖n p_{Ak}(B) \; ✕ \; p(A_k)$

➨On fais la somme des toutes les probabilités des branches de l'arbre qui mènent au résultat désiré

Evenements indépendants

Carcatéristiques pratiques

Deux évènements sont indépendants s si la réalisation de l'un n'influe pas sur la réalisation de l'autre

➥Quand un évènement se réalise, cela ne change pas la probabilité que l'autre évènement arrive

Formule de l'indépendance

Deux évènements A et B sont indépendants s si: p(A∩B) = p(A) ✕ p(B)

Propriétés de l'indépendance

Pour deux évènements A et B de probabilités non nulles

Si A et B sont indépendants s alors:

p_B(A) = p(A)

p_A(B) = p(B)

p_B(A) = p_$\ov{B}$(A)

p_A(B) = p_$\ov{A}$(B)

$\ov{A}$ et B sont indépendants

A et $\ov{B}$ sont indépendants

$\ov{A}$ et $\ov{B}$ sont indépendants

Preuve:

p(A) = p(A∩B)+p(A ∩ $\ov{B}$) = p_B(A) ✕ p(B)+p_$\ov{B}$(A) ✕ p($\ov{B}$)

On utilise l'hypothèse: p_B(A) = p_/B(A) et on l'injecte dans l'équation, on a donc:

p_B(A) ✕ p(B)+p_B(A) ✕ p($\ov{B}$)

= p_B(A) ✕ (B+$\ov{B}$)

= p_B(A)

Partagez ce cours !

Suivez Nicolas KRITTER sur google + ( cours inspiré de celui fait par le professeur de la classe)