Les nombres complexes

Introduction aux nombres complexe
Définition de i
On créée une entité mathématique noté i tels que:
i² = -1
On utilise avec i les mêmes règles algébriques qu'avec un nombre réel
Exemples de calculs avec les nombres complexe
i3 = -i
i4 = 1
Exemple d'équations résolues avec des nombres complexe
x²+1 = 0 pour x = i (car i² = -1) ou x = -i (car (-i)² = i
Comme x²+1 = x²-i², on factorise sous la forme (x-i)(x+i)
x² = - 4, on a donc x²+4 = 0 pour x = 2i ou x = -2i
Et x²-4 = x²-(2i)²
Résolutions d'équations simple avec "i"
k ∈R et k>0
L'équation x² = -k a deux solutions:
x = i√(k)
x = -i√(k)
Définitions des nombres complexes
Un nombre complexe est un nombre z qui peut s'écrire sous la forme:
z = a+ib
Avec a ∈R, b ∈ R et i est un nombre complexe: i² = -1
Cette forme s'appel la forme algébrique
a s'appel la partie réel de z
b s'appel la partie imaginaire de z
Notation:
On note a = Re(z)
On note b = Im(z)
Ensemble de définition des nombre complexe
On note l'ensemble de définition des nombres complexe C
C = {z} tel que z = a +ib et a ∈R, b ∈R et i² = -1
REMARQUE: R est inclus dans C et z ∈R si: z = a+ib avec b = 0
z ∈ C donc:
Im(z) = 0 équivaut à z ∈ R
Re(z) = 0 équivaut à z est un imaginaire pur
Propriété
z = 0 équivaut à Re(z) = Im = 0
Ce qui veut dire que si a+ ib = 0, a = 0 et b = 0
Règles des nombre complexe
Règle:
Un polynôme à coefficient complexe (= nombre complexe) d'une variable complexe (=x est un nombre complexe) a les même propriétés que les polynômes à coefficient réel d'une variable réelle (= x est un réel)
Somme et produit de nombres complexe
Exemple: z = 2+3i et z' = -1+4i
z+z' = 2+3i + (-1+4i) = 2-1 +3i+4i = 1+7i
z ✕ z' = (2+3i) ✕ (-1+4i) = -2+8i-3i-12 = -14-5i
Généralisation des produits et sommes de nombres complexe
Avec z = a+ib et z' = a'+ib'
z+z' = a+a'+i(b+b')
z ✕ z' = a ✕ a'-b ✕ b'+i(ab'+a'b)
Rapport de deux nombres complexes
(a,a',b,b')∈R4, z = a+ib et z' = a'+ib'
Conjugué d'un nombre complexe
Le conjugué d'un nombre complexe z se note $\ov{z}$
Pour z = a+ib
On a: $\ov{z}$ = a-ib
Propriétés
Re$\ov{z}$ = Re(z)
Im$\ov{z}$ = -Im(z)
➥Si z' = $\ov{z}$, alors on a: a' = a et b' = -b
Avec a,a',b,b' ∈R
Module d'un nombre complexe
Le module d'un nombre complexe z est noté |z|
Pour z = a+ib
On a: |z| = √(a²+b²)
Propriétés
z ✕ $\ov{z}$ = (a+ib) ✕ (a-ib) = a²-(-ib)² = a²+b² = |z|²
z∈R et |z|≥0
REMARQUE: si z∈R, z = a+ib et b = 0
|z| = √(a²+0²) = √(a²)
Donc quand b = 0, |z| vaut la valeur absolue de a
-
Inverse d'un nombre complexe
Pour prendre l'inverse d'un nombre complexe, on multiplie par le conjugué du dénominateur en haut et en bas
On a donc: $ {1}/{z} = {\ov{z}}/{|z|^2}$
Ce qui donne: $ {1}/{a \; + \; ib} = {1 \; ✕ \; (a-ib)}/{(a \; + \; ib) \; ✕ \; (a-ib)} = {a-ib}/{a^2 \; + \; b^2}$
Écriture algébrique d'un quotient
On utilise la même propriété que pour l'inverse
On multiplie en haut et en bas par le conjugué du dénominateur
Ce qui donne:
$ {z}/{z'} = {z \; ✕ \; \ov{z'}}/{|z'|^2}$
On a donc: $ { a \; + \; ib}/{a' \; + \; ib'} = {(a \; + \; ib) \; ✕ \; (a' -ib')}/{a'^2 \; + \; b'^2}$
ATTENTION: quand on a une forme 2+i, a = 2 et b = 1 car on a: 2+1 ✕ i
Résoudre une équation du second degré à coefficient réel et delta négatif
Pour résoudre une équation du second degré avec delta négatif, on utilise la même méthode que pour le delta positif
Par contre, on obtient les 2 solutions suivantes:
x1 = ${-b -i √{| Δ |}}/{2a}$ et x2 = ${-b \; + \; i √{| Δ |}}/{2a} $
On factorise donc de la façon suivante:
$a(x-(-b - i√(|Δ|))/{2a}) \; ✕ \;(x-(-b + i√(|Δ|))/{2a})$
Identités remarquables
a3-b3 = (a-b)(a²+ab+b²)
a3+b3 = (a+b)(a²-ab+b²)
(a+b)3 = a3+3a²b+3ab²+b3
(a-b)3 = a3-3a²b+3ab²-b3
Propriétés des conjuguées et des modules
Avec z et z', 2 nombres complexe
Calculs avec les conjugués
${\ov{z}}↖ {-} = z$
Multiplication et conjugués:
$ z\; ✕ \; \ov{z}$ = |z|²
$\ov{(z \; ✕ \; z')} = \ov{z} \; ✕ \; \ov{z'}$
Divisions et conjugués
$\ov{(z/z')} = \ov{z}/{z'}↖ {-}$
Additions et multiplications
$\ov{(z+z')} = \ov{z} \; + \; \ov{z'}$ et $\ov(z-z') = \ov{z} \; - \; \ov{z'}$
Relation avec la puissance
${\ov{z}}^2 = \ov{(z^n)}$
➨Le conjugué d'une opération avec z et z' équivaut à la même opération avec les conjugués de z et de z'
Relation entre z et son conjugué
Si $\ov{z}$ = z alors z est un réel
➥car le b de z = a+ib est nul
Si $\ov{z}$ = -z, alors z est un imaginaire pur
➥car le a de z = a+ib est nul
Rez = $(z+\ov{z})/2$
➥ z+$\ov{z}$ = 2Rez
Imz = $(z-\ov{z})/2$
➥ z-$\ov{z}$ = 2Imz
Propriétés des modules
|$\ov{z}$| = |-z| = |z|
|z| = 0 équivaut à z = 0
Calculs avec les modules
Multiplication et modules
|z ✕ z'| = |z| ✕ |z'|
Division et module
$|z/{z'}|$ = ${|z|}/{|z'|}$ pour tout z différent de 0
Relation avec les puissances
|zn| = |z|n
Inégalité triangulaire
Comme on peut assimiler z à un vecteur, on obtient l'inégalité suivante
|z+z'|≤|z|+|z'|
➥Ce qui équivaudrait à la norme du vecteur z+z' est inférieur ou égal à la norme du vecteur z + la nombre du vecteur z'
Comme |z| = √(a²+b²) on a:
Rez ≤ |z| et Imz ≤ |z|
Représentation trigonométrique des nombres complexes
Plan complexe
-Soit un plan muni d'un repère orthonormé o,i,j
On peut associer un nombre complexe à un point
-La coordonné d'un nombre complexe z = a+ib équivaut à la coordonné d'un point M (a,b) dans le plan o,i,j
M est alors l'image de z
z est alors l'affixe du point M
Le point M définit par l'affixe z se note: Mz
Affixe d'un vecteur
On peut aussi associer un nombre complexe à un vecteur, et réciproquement
On associe un vecteur u(x;y) a un nombre complexe z= x + iy
Soit 2 points A(xa;ya) et B(xb;yb)
Soit zA l'affixe de A et zB l'affixe de B
On a donc zAB l'affixe du vecteur AB
Relation: zAB = zB-zA
RAPPEL: Les coordonnées du vecteur AB sont: (xb-xa;yb-ya)
Colinéarité de deux vecteurs s
Deux vecteur u et v non nul sont colinéaires si et seulement si:
il existe un k ∈R tels que v = k ✕ u
Pour les affixes:
v un vecteur d'affixe z
u un vecteur d'affixe z'
On a donc: si u et v sont colinéaires:
il existe un k ∈ R tels que: z = k ✕ z'
➥ Donc $z/{z'}$ ∈R
Propriétés
Soit: zA l'affixe du point A
Soit: zB l'affixe du point B
On a donc:
|zA| = OA
|zB-zA| = AB
Soit z l'affixe du point Mz
Soit $\ov{z}$ l'affixe du point M$\ov{z}$
On a donc le point M$\ov{z}$ est le symétrique de Mz par rapport à l'axe OX
➥ $\ov{z}$ est le conjugué de z
Soit z1 l'affixe du point M1
Si z1 = -z, alors M1 est le symétrique de M par rapport à l'axe OX
I est le milieu de AB, donc zI = $(z_A+z_B)/2$
Forme trigonométrique d'un nombre complexe
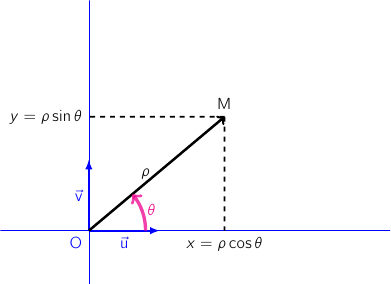
Un repérage dans le plan: le repérage polaire
On a les relations:
xm = r ✕ cos(θ)
ym = r ✕ sin(θ)
Remarque: dans la définition exacte des coordonnées polaire, R peut être négatif
Forme trigonométrique
Soit le nombre complexe z = a +ib, avec a et a 2 réels
Soit M l'image de z dans le plan complexe
M a pour coordonnées cartésienne: (a;b)
Soit: r et θ, les coordonnées polaire de M
r: le rayon, θ: l'angle entre le rayon et l'axe des abscisses s
On a donc: z = a +ib = z = r ✕ cos(θ)+r ✕ i ✕ sin(θ)
Propriétés et définitions
Tout nombre complexe z peut s'écrire sous la forme:
z = r(cos(θ) + i (sinθ))
➥r ∈R² et θ ∈R
cette forme s'appelle la forme trigonométrique
θ s'appelle l'argument de z, noté argz = θ
r est le module de z, on le note |z|
REMARQUE: il y a une infinité d'arguments de z, car on a comme argument: θ [2kπ]
z = 0 n'as pas d'arguments
Relation entre forme algébrique et forme trigonométrique
comme z = a+ib = r ✕ (cos(θ)+i ✕ sin(θ)), on a:
a = r ✕ cos(θ) et b = r ✕ sin(θ)
De plus, r = |z| = √(a²+b²)
Ce qui donne:
cos(θ) = $a/r = a/√(a²+b²)$
et sin(θ) = $b/r = b/√(a²+b²)$
Argument d'un conjugué
L'argument d'un conjugué : $\ov{z}$ est l'opposé de l'argument de z
On a: argz = θ [2π] donc arg $\ov{z}$ = -θ [2π]
Nombres complexes égaux
Soit 2 nombres complexe:
z = R(cos(θ) +i ✕ sin(θ)) et z' = r'(cos(θ')+i ✕ sin(θ'))
z = z' si:
r = r' ET θ = θ'+2kπ
Argument d'un produit
Produit de deux nombres complexes: z et z'
z ✕ z' = r(cos(θ)+i ✕ sin(θ)) ✕ r'(cos(θ')+i ✕ sin(θ'))
➨ z ✕ z' = r ✕ r' ✕ [(cos(θ) ✕ cos(θ')-sin(θ) ✕ sin(θ'))+i ✕ (sin(θ') ✕ cos(θ)+cos(θ') ✕ sin(θ))]
On retrouve ici les formes cos(a+b) et sin(a+b)
On a donc: z ✕ z' = r ✕ r' ✕ (cos(θ+θ')+i ✕ sin(θ+θ'))
Ce qui fait que: arg(z ✕ z') = argz+argz' [2π]
Et pour tout n ∈N*, on a: arg(zn) = n ✕ argz [2π]
Argument d'un quotient
L'argument d'un quotient de deux nombres complexe z et z'
arg ($z/{z'}$) = argz-argz'
On a donc: arg($1/z$) = -argz' [2π]
Notation exponentielle
Définition
On admet la relation suivante:
cos(θ)+i ✕ sin(θ) = ei ✕ θ
➥ le "e" est le "e" de fonction exponentielle
Cette relation permet donc d'écrire tout nombre complexe non nul de la façon suivante:
z =r✕ei ✕ θ
Avec r: le module de z, notée |z| et θ: l'argument de z notée
REMARQUE:
2 ✕ ei ✕ ($π/6$) →|z| = 2 et θ = $π/6$
Mais: -2 ✕ ei ✕ ($π/6$) ⇒|z| = 2 et θ = -$π/6$
Propriétés de la notation exponentielle
Quelque soit θ ∈ R: |eiθ| = 1
Pour tout z et $\ov{z}$ différents de 0, pour r∈ R
z =r✕eiθ donc $\ov{z}$ =r✕e-iθ car arg (z) = - arg ($\ov{z}$) et |z| = |$\ov{z}$|
Multiplication:
z ✕ z' = r ✕ r'i(θ+θ') =r ✕ eiθ ✕ r' ✕ eiθ'
On a cette forme car |z ✕ z'| = |z| ✕ |z'| et arg (z ✕ z') = arg z + arg z'
Division
${z}/{z'} = {r}/{r'} \; ✕ \; e^{i(θ -θ ')} = {r\; ✕ \; e^{iθ}}/{r'\; ✕ \; e^{iθ '}}$
Inverse
$1/z = (1/r)$ ✕ e-iθ = $1/{r \; ✕ \; e^{iθ}}$
Car: |$1/z$| = $1/{|z|}$ et arg($1/z$) = -arg z
Puissance
Pour tout n∈N: zn = rn ✕ ei ✕ n ✕ θ = (r✕eiθ)n
Formule d'Euler
On admet: eiθ = cos(θ) +i ✕ sin(θ)
Et: e-iθ = cos(θ) -i ✕ sin(θ)
Ce qui donne les relations:
eiθ+e-iθ = 2 ✕ cos(θ)
eiθ-e-iθ = 2 ✕ sin(θ)
Ce qui permet de calculer cos(θ) et sin(θ) avec les relations:
cos(θ) = $(e^{iθ}+e^{-iθ})/2$
sin(θ) = $(e^{iθ}-e^{-iθ})/2$
Formule de Moivre
Formule du mathématicienMoivre:
(eiθ)n = (en ✕ iθ)
On a donc: (cos(θ)+i ✕ sin(θ))n = cos(n ✕ θ)+i ✕ sin(n ✕ θ)
Partagez ce cours !
Suivez Nicolas KRITTER sur google + ( cours inspiré de celui fait par le professeur de la classe)