Géométrie pure dans l'espace|cours de maths terminale

Un objet dans l'espace est un objet en volume, il est en trois dimensions

Un problème: comment représenter un objet en trois dimension dans un plan en 2 dimensions

Quelques solutions de représentation de perspective en mathématiques (en art, on utilise en plus la couleur, lumière...)

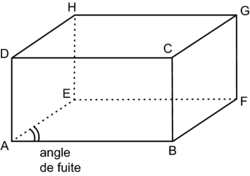
La perspective cavalière

La perspective cavalière conserve le parallélisme

➥On dessine les contours de la forme visible en trait pleins et les contours "cachés" en pointillés

-On décale les faces

Pour les sphères, on dessine un équateur en forme d'ellipse

Exemple: un pavé en perspective cavalière

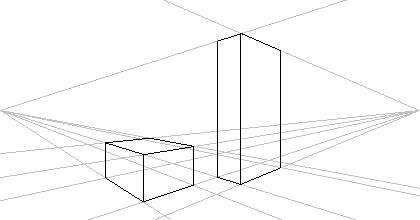
La perspective à points de fuite

Le point de fuite est le point où semble converger toutes les parallèles du solide

Exemple: quand on regarde des rails de trains au loin, elles semblent converger vers un point alors qu'elles sont parallèle

Un écueil à ne pas faire: les perspectives impossibles

Quand on respecte pas les règles mathématiques de la perspective, on peut créer des objets impossible

➥Ce sont des figures paradoxales (on joue sur les plans)

Exemple: L'escalier qui monte et qui descend

Maurits Escher, un maître de la perspective impossible

Les principaux objets de l'espace

Les principaux objets de l'espace sont: le point , la droite et le plan

Caractéristiques d'un plan

On peut définir un plan de 3 manières:

- 3 points non alignés

- 1 points et 1 droite de passant pas par ce point

- 2 droites sécantes

- 2 droites parallèles et non confondues

Propriété: pour tout point A et B non confondue et un plan P

➥ Si A ∈ P et B ∈ P alors AB ∈ P

Position, relation de 2 plans

Définition et propriété:

2 plants sont sécant s'ils se coupent selont une droite unique

Position relative d'une droite et d'un plan

Définition et propriété 1

Une droite et un plan sont sécant s'ils se coupent en un point unique

Définition et propriété 2

Une droite et un plan sont parallèles s'ils n'ont aucun point en commun ou si la droite est contenue dans le plan

Position relative de 2 droites, coplanairité

Défnition de la coplanairité

Deux droites sont coplanaires S'il existe un plan qui contient ces 2 droites

Propriété de deux droites coplanaires

Deux droites sont coplanaire si elle sont sécantes ou parallèle

Parallélisme dans l'espace

P et P' sont deux plans

D et D' sont deux droites sécantes de P

Propriétés du parallélisme deux deux plan

Si P//P' alors toutes les droites de P sont parallèle à P'

Si D//P' et D'//P alors P//P'

P et D sont parallèle si et seulement S'il existe une droite D' du plan P telle que: D'//D

Orthogonalité dans l'espace

Orthogonalité de deux droites

Définition de l'orthogonalité de deux droites

Deux droites sont orthogonales si leurs parallèles passant par un point sont perpendiculaires

Orthogonalité entre une droite et un plan

Définition de l'orthogonalité entre une droite et un plan

Une droite et un plan sont perpendiculaire si la droite est perpendiculaire à toutes autres droites du plan

Propriété

D₁ et D₂ sont deux droites sécantes d'un plan P

Si une droite est perpendiculaire à D₁ est D ₂ alors cette droite est perpendiculaire au plan P

Plan perpendiculaire

Définition

P et P' sont perpendiculaire si un des plan contient une droite perpendiculaire à l'autre

Plan médiateur

Le plan médiateur d'un segment [AB] est l'ensemble des points qui sont équidistant à A et à B

Propriété: Le plan médiateur d'un segment [AB] est perpendiculaire à[AB] et passe par son milieu

-

Partagez ce cours !

Suivez Nicolas KRITTER sur google + ( cours inspiré de celui fait par le professeur de la classe)